

So without further ado, let’s learn some cool math! Thus, based on the measure, we can actually identify which frequencies of oscillations were used to construct our original signal! While this might not make sense yet, if you bear with me to the end of the post, it will hopefully become more clear. In practice, we can use this notion to sweep over a range of frequencies, and quantify how dominant each particular frequency is within the original signal. strength of prevalence) of a particular frequency within a signal. The Fourier Transform equation is essentially a measurement of the energy (i.e. But in all seriousness, if we break it down and visualize how this expression manipulates the data, seemingly complex expression can actually become quite intuitive!īefore I jump into the math explanation, a high level overview of where we are going in english might be helpful. Within the manuscript, Fourier details his “signal sifter” using the following equation:Īt first glance, and as any biologist can tell you, the math looks overly complicated and downright scary! And while Σ and π might be the only greek letters, there is definitely grounds for glossing over the above equation and saying “ It’s all in Greek to me…“.
FOURIER TRANSFORM EQUATION HOW TO
While coming up with how to build this machine in a mathematical framework is not trivial, fortunately, a solution was created in the 1820’s by a French Mathematician/Physicist by the name of Joseph Fourier in his seminal work: Théorie analytique de la chaleur ( The Analytical Theory of Heat). This unmixing problem is what Fourier Transforms will try to solve.Ī potential solution to our mixed signal problem would be to create a sort of mathematical “signal sifter” to pull out each individual signal from our mixed signal. However, in signal processing we are just given the green signal and need to discover the yellow and blue in order to extract useful information such as signal frequency, amplitude, and period. For instance, if we add the yellow signal below to the blue signal, we produce the green signal. What colors would you mix and how much of each? Not as easy anymore is it? This problem of determining the components of a mixed paint color is analogous to a fundamental problem in signal processing. Moreover, what if you were bored of the green paint and wanted to make a beige, magenta, or even salmon colored paint. This might seem trivial since most people know that yellow and blue make green, but you still might not know the correct ratio of blue to yellow to add in order to recreate the exact green color. Naturally wanting more of it, you wonder which colors were originally mixed together to create it.
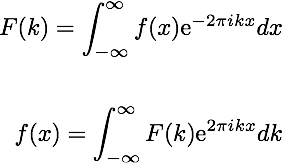
Let’s say your favorite bucket of green paint is almost empty. I’ll start out by presenting a quick analogy. While Fourier Transforms were originally developed to solve problems related to heat transfer within the field of physics the math behind it has found many uses in biology, robotics, finance, and even the music industry! Basically, I think Fourier Transforms are an incredibly cool and useful form of mathematics, so my goal in this post will be to share with you what I find so fascinating in a way that I hope is comprehensible and helps develop an intuition for how they work. One of the potential solutions that I am going to explain today comes in the form of a type of math known as Fourier Transforms. My research has thus brought me to learn some math that allows these amplitude, frequency, and period measurements to be computed automatically using a computer. Naturally, things become a bit more complicated and far too time consuming to do by hand. While in the image below it might be easy to read these measurements by eye, in reality, I am working with 11,000-20,000 makers at once. Often, it is useful to quantify different aspects of a given circadian marker such as the frequency, period, and amplitude of the signals oscillation. Mainly, I might be looking at the expression of a gene or biomarker over the course of the day, such as melatonin levels seen in the image below.
FOURIER TRANSFORM EQUATION SERIES
As a computational biologist that studies circadian rhythms, often times I am found analyzing time series data.


 0 kommentar(er)
0 kommentar(er)
